The genetic code seems to not be enough to describe the complexity of a human being. In fact, it seems too small to describe most of the life forms. We could assume that the genetic code has all the information very compressed, but still...
I will approach the problem of describing life complexity based of information theory.
DNA and bits
A DNA sequence is a string of pairs. There are 4 pairs (T,A,C,G). We can encode each of there pairs by binary numbers 00,01,10,11. In the rest of the argument, I will use bits in order to analyze how DNA could represent a compressed information. For a more intuitive understanding, I will use terms like "files", "strings" or "binary sequences", depending on the context, with the same meaning. At the end, we will move back from bits to DNA sequences.
About compression
In simple words, a compressed string of bits (see a file) is a self-extracting archive that can be transformed into the initial string - by running that self-extract archive.
This is a more general definition than the usual compressing algorithms (zip) do. For example, most compressing algorithms will probably not compress in less than 10% of the initial size the first billion decimals of the "square root of two" (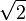
= 1,4142135623...), however you can make a very short program to generate as many decimals as you want.
In this more general definition, any sequence of bits that can be generated by a simple program is very compressible. In particular, the program could be a specific un-compressing algorithm paired with his compressed input. Therefore, this definition is including what a regular compression algorithm does. However, in this more general definition, the size of the compressed string/file includes the length of the un-compressing program, including any input you may need (you can include the "compressed file" in the program's constants). A more formal definition is the Kolmogorov complexity.
How well can be something compressed?
Actually, you cannot compress everything less than the original size. In general, in order to compress all the files (strings) of N bits, you need, on average, at least N bits for each compressed version. Some compressions will take for example N/2 bits, but other will take at least N+1 bits. This is because for each file/string to be compressed you need an unique "compressed" version. There are 2^N possible files, you cannot create 2^N unique compression values using less than N bits for each. A more formal and general proof can be found Shannon's source coding theorem.
The compression issue is in knowing where to stop
Actually, you can create any given bits sequence with a very simple program. For example you can create a program that is iterating all the numbers: 0,1,2,3,... and generate the binary representation of each such number, concatenated. You are not limited to the size of the fundamental data types (like "long long int"), you can store a big string of bits in memory and increment your huge number with simple operations on bits.
Given an infinite data type and time, this "universal generator" will generate all the possible bits combinations. After a long enough time, the program will generate the number that has the binary representation of any Shakespeare novel you take. It's like the infinite monkey theorem, except that you can actually calculate when the process will end.
After a long time, this huge string will contain the representation of all the files in your computer, all the documents, all the music files and movies. Practically, it can generate any digitized representation of anything in Universe.
So, in fact, you have a way to generate with a software program any binary information you could imagine. You can loop through all the numbers and only print the number that has the binary representation of the information you want to compress. The program is very simple in terms of algorithm, just that... it's hard to describe when the program reached that number. Actually, in order to put that stop number into program, you need to represent it somehow, and for this you need in average the same number of bits you want to compress.
There are cases when there is a very simple program that generates a very (apparent) complex string of bits (like the "squared root of two" example). We will consider this kind of strings as "very compressible". Shannon theorem tells us that there are other strings that cannot be compressed in less than N+1 bits. You can always compress in at most N+1 bits (except the un-compressing code): use the additional "+1" bit to just say "I could not compress this file in less than N bits, I put it here uncompressed, just print it".
The Universe as bits
We can imagine a very huge string that describes a portion of Universe, like our solar system, or just the Earth.
It does not need to describe all the details (see uncertainty principle), just enough information about atoms position to be able to reconstruct that region of Universe sufficiently alike. Remember that the final subject is DNA, it's likely that DNA does not describe where each electron will be in the resulting living being, just a general scheme on how atoms and cells will organize.
With this bits representation of the Universe region, each being may be a sub-string of this representation. So what?...
The string regions
Let's go back to the "universal generator", the program that is able to generate all the possible bits combinations somewhere in the huge string it generates. It is enough to know where to start in this string in order to be able to retrieve any given information (like that Shakespeare novel, an HD movie or... the representation of that portion of the Universe).
The heresy
It's hard to KNOW where to start, it's like knowing that information in the first place. But what if you ARE in that place already? Let's say that a very big portion of the Universe is the generated string, and you happen to BE in that specific area of this string, that contains the information you need?
For simplicity, we can consider that portion of Universe as "the Universe", even if it's a weak, binary representation of the Universe. This Universe can be arbitrarily big, it can contains all the information you may think of. It contains that Shakespeare novel, the HD movie, and even the placement of each atom in a living being. Well, this is not so spectacular, by definition that Universe contains the living beings that are contained in it.
Hmm, but what if there is a general scheme of creating a (human) being in this Universe, and we are just in the right place to access it? In this case you don't need to encode in the DNA all the details of creating that being, you just need to select some predefined programs that exists in that Universe's fabric.
I am not thinking about supernatural beings, esoteric or transcendental/conscientious Universe. Maybe it's just the combination of physics laws in this corner of the Universe favorable for combining the atoms into life. The DNA only needs to select from some pre-existing (let's say) forms of life. Pre-existing means they are easily obtained starting with the local bits, in the same way as the complexity of the "squared root of two" decimals sequence is easily generated with a simple program.
(to be continued)
I will approach the problem of describing life complexity based of information theory.
DNA and bits
A DNA sequence is a string of pairs. There are 4 pairs (T,A,C,G). We can encode each of there pairs by binary numbers 00,01,10,11. In the rest of the argument, I will use bits in order to analyze how DNA could represent a compressed information. For a more intuitive understanding, I will use terms like "files", "strings" or "binary sequences", depending on the context, with the same meaning. At the end, we will move back from bits to DNA sequences.
About compression
In simple words, a compressed string of bits (see a file) is a self-extracting archive that can be transformed into the initial string - by running that self-extract archive.
This is a more general definition than the usual compressing algorithms (zip) do. For example, most compressing algorithms will probably not compress in less than 10% of the initial size the first billion decimals of the "square root of two" (
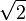= 1,4142135623...), however you can make a very short program to generate as many decimals as you want.In this more general definition, any sequence of bits that can be generated by a simple program is very compressible. In particular, the program could be a specific un-compressing algorithm paired with his compressed input. Therefore, this definition is including what a regular compression algorithm does. However, in this more general definition, the size of the compressed string/file includes the length of the un-compressing program, including any input you may need (you can include the "compressed file" in the program's constants). A more formal definition is the Kolmogorov complexity.
How well can be something compressed?
Actually, you cannot compress everything less than the original size. In general, in order to compress all the files (strings) of N bits, you need, on average, at least N bits for each compressed version. Some compressions will take for example N/2 bits, but other will take at least N+1 bits. This is because for each file/string to be compressed you need an unique "compressed" version. There are 2^N possible files, you cannot create 2^N unique compression values using less than N bits for each. A more formal and general proof can be found Shannon's source coding theorem.
The compression issue is in knowing where to stop
Actually, you can create any given bits sequence with a very simple program. For example you can create a program that is iterating all the numbers: 0,1,2,3,... and generate the binary representation of each such number, concatenated. You are not limited to the size of the fundamental data types (like "long long int"), you can store a big string of bits in memory and increment your huge number with simple operations on bits.
Given an infinite data type and time, this "universal generator" will generate all the possible bits combinations. After a long enough time, the program will generate the number that has the binary representation of any Shakespeare novel you take. It's like the infinite monkey theorem, except that you can actually calculate when the process will end.
After a long time, this huge string will contain the representation of all the files in your computer, all the documents, all the music files and movies. Practically, it can generate any digitized representation of anything in Universe.
So, in fact, you have a way to generate with a software program any binary information you could imagine. You can loop through all the numbers and only print the number that has the binary representation of the information you want to compress. The program is very simple in terms of algorithm, just that... it's hard to describe when the program reached that number. Actually, in order to put that stop number into program, you need to represent it somehow, and for this you need in average the same number of bits you want to compress.
There are cases when there is a very simple program that generates a very (apparent) complex string of bits (like the "squared root of two" example). We will consider this kind of strings as "very compressible". Shannon theorem tells us that there are other strings that cannot be compressed in less than N+1 bits. You can always compress in at most N+1 bits (except the un-compressing code): use the additional "+1" bit to just say "I could not compress this file in less than N bits, I put it here uncompressed, just print it".
The Universe as bits
We can imagine a very huge string that describes a portion of Universe, like our solar system, or just the Earth.
It does not need to describe all the details (see uncertainty principle), just enough information about atoms position to be able to reconstruct that region of Universe sufficiently alike. Remember that the final subject is DNA, it's likely that DNA does not describe where each electron will be in the resulting living being, just a general scheme on how atoms and cells will organize.
With this bits representation of the Universe region, each being may be a sub-string of this representation. So what?...
The string regions
Let's go back to the "universal generator", the program that is able to generate all the possible bits combinations somewhere in the huge string it generates. It is enough to know where to start in this string in order to be able to retrieve any given information (like that Shakespeare novel, an HD movie or... the representation of that portion of the Universe).
The heresy
It's hard to KNOW where to start, it's like knowing that information in the first place. But what if you ARE in that place already? Let's say that a very big portion of the Universe is the generated string, and you happen to BE in that specific area of this string, that contains the information you need?
For simplicity, we can consider that portion of Universe as "the Universe", even if it's a weak, binary representation of the Universe. This Universe can be arbitrarily big, it can contains all the information you may think of. It contains that Shakespeare novel, the HD movie, and even the placement of each atom in a living being. Well, this is not so spectacular, by definition that Universe contains the living beings that are contained in it.
Hmm, but what if there is a general scheme of creating a (human) being in this Universe, and we are just in the right place to access it? In this case you don't need to encode in the DNA all the details of creating that being, you just need to select some predefined programs that exists in that Universe's fabric.
I am not thinking about supernatural beings, esoteric or transcendental/conscientious Universe. Maybe it's just the combination of physics laws in this corner of the Universe favorable for combining the atoms into life. The DNA only needs to select from some pre-existing (let's say) forms of life. Pre-existing means they are easily obtained starting with the local bits, in the same way as the complexity of the "squared root of two" decimals sequence is easily generated with a simple program.
(to be continued)
Comments